NUS scientists have predicted a new type of nonequilibrium effects that could generally exist in nanoscale electronic devices, and successfully explained a recent puzzling experiment using the effects.
The research group led by Prof ZHANG Chun from the Department of Physics and the Department of Chemistry, National University of Singapore, studied the theoretical transport properties of silane junctions building on the steady-state DFT technique that was proposed by Prof Zhang himself back in 2015. The steady-state DFT considers nonequilibrium effects in full by employing nonequilibrium quantum statistics. They found that underlying the puzzling experimental observations is a novel type of nonequilibrium effects (named “nonequilibrium pulling” in their work) that exist in silane junctions having thiol linkers. Their theoretical calculations show that, when the junction is near equilibrium, the standard DFT method is an excellent approximation of steady state conditions. However, at low biases around the region of 0.2 volts, the “nonequilibrium pulling” effect drives the thiol-terminated silanes far away from equilibrium, thus resulting in the reversal of conductance values observed in experiments.
Prof Zhang said, “Further analysis suggests that these nonequilibrium effects could generally exist in nanoscale devices in which there are conducting channels mainly residing at the source contact and located close to the bias window. These findings significantly broaden our fundamental understanding of electron transport at the nanoscale.”
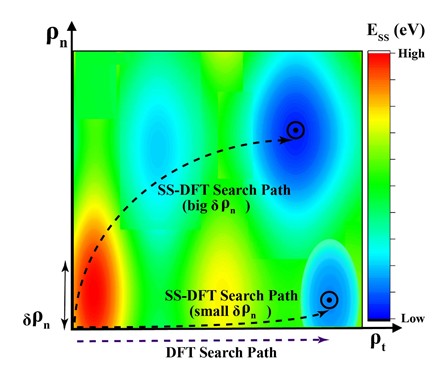
The figure shows the conceptual difference between steady-state DFT (used by the research team) and the standard DFT method. In steady-state DFT, the transport state is a functional of two densities, the total electron density ρt and the current-carrying electron density ρn. The standard DFT can be considered to be “one-dimensional” as the transport state is only determined by ρt. The two-dimensional (2D) colour contour represents the energy of the steady-state transport state Ess. Steady-state DFT searches for the most stable transport state in the 2D plane (global minimum energy state) while the standard DFT does the search along ρt axis (local minimum energy state). When the system is near equilibrium, ρn is small and the search path of the steady-state DFT is close to the ρt axis. For such cases, the standard DFT method can be a good approximation. [Credit: Nanoscale Horizons]. Read the full story here.
